- Kirjoittaja admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:20.
- Viimeksi muokattu 2025-06-01 06:12.

Esimerkkejä kultaisesta suhteesta löytyy kaikki alta klassisesta arkkitehtuurista, taiteesta, luonnosta ja jopa musiikista. Tämä suhteiden ilmaisu, joka tunnetaan myös nimellä jumalallinen suhde, tarjoaa harmonisen koostumuksen käyttämällä irrationaalista lukua (1,618) suunnittelussa, sekä luonnollisessa että ihmisen tekemässä. Todennäköisesti et ole tietoinen Kultaisen Suhteen kauneuden takana olevasta matematiikasta, koska se tuottaa esineitä ja musiikkia, jotka ovat sinulle luonnollisesti miellyttäviä ilman selityksiä.
Arkkitehtuurin kultainen suhde
Kultainen suhde luo lähes täydellisen kauneuden luonnossa ja taiteessa. Kun alat etsiä Golden Ratio -esimerkkejä jokapäiväisessä elämässä, saatat yllättyä monista tapauksista, joissa sitä on käytetty monien monumentaalisten rakennusten ja rakenteiden luomiseen. Kun kultaista suhdetta käytetään arkkitehtuurissa, rakennuksen sanotaan luovan "pyhää arkkitehtuuria". Soveltamalla kultaisen suhteen laskentaa neliöön arkkitehdit ja suunnittelijat voivat luoda kultaisen suorakulmion, jonka uskotaan olevan esteettisesti miellyttävimmät mittasuhteet ihmissilmälle.
Kultainen suorakulmio Esimerkki: Parthenon

Kreikkalainen kuvanveistäjä Phidias käytti töissään kultaista suhdetta, varsinkin kun hän alkoi työskennellä juuri Parthenon-pylväiden yläpuolelle veistettyjen nauhojen kanssa. On myös tärkeää huomata, että kultaiselle suhteelle annettu numeerinen arvo Phi nimettiin hänen kunniakseen.
Jos mittaat Parthenonin ulkopinnan mitat, huomaat, että se ei vain muodosta kultaista suorakulmiota, vaan että pylväiden välissä on myös monia kultaisia suorakulmioita. Tämä pyhä rakennelma on kaunis esimerkki arkkitehtuurin kultaisesta suhteesta.
Kultainen kolmio Esimerkki: Gizan suuri pyramidi
Kultainen suhde, kultainen suorakulmio ja kultainen kolmio löytyvät kaikki yhden maailman seitsemästä ihmeestä, Gizan suuresta pyramidista, täydellisyydestä. Kultaisen suhteen selvittämiseksi sinun on puolitettava pyramidin neliömäinen kanta ja piirrettävä pystysuora viiva pyramidin keskustaan. Kun tämä on yhdistetty pyramidin kulmaan, voit helposti nähdä, kuinka se muodostaa kultaisen kolmion, jonka suhde on 1,618, kultaisen suhteen.
Muut arkkitehtoniset esimerkit
Löydät monia esimerkkejä muinaisesta nykyaikaiseen pyhään arkkitehtuuriin ja Golden Ratio -rakennuksiin.
- Chartres Cathedral - Centre, Ranska
- Notre Dame - Pariisi, Ranska
- Porch of Maidens - Akropolis, Ateena
- Taj Mahal - Agra, Intia
- Yhdistyneiden kansakuntien rakennus - New York City, New York
Kultainen suhde taideesimerkeissä
Löydät monia esimerkkejä maalareista, jotka käyttivät kultaista suhdetta. Nämä täydellisyydet luotiin käyttämällä kultaisten suorakulmioiden ja kultaisten kolmioiden suhdetta. Kultaisen suorakulmion pohj alta luotu taide osoittautuu ihmissilmälle miellyttävämmäksi. Se on yksi mysteereistä, jotka ympäröivät tätä täydellistä suorakulmiota ja kultaista suhdetta.
Kultainen suhde taiteessa

Kultaisen suhteen taideesimerkkejä ovat:
- Leonardo Di Vinci - Mona Lisa, Vitruvian Man
- Botticelli - Venuksen syntymä
- Michelangelo - Pyhä perhe, 'Daavid'
- Rafael - Ristiinnaulitseminen
- Rembrandt - Omakuva
- Salvador Dali - Viimeisen ehtoollisen sakramentti, Muistin pysyvyys
Kultaisen suhteen käyttäminen taideteoksessa
Kultaisen suorakulmion sisällä on tiettyjä alueita, joiden on havaittu olevan visuaalisesti houkuttelevampia kuin muut alueet. Nämä pisteet löydetään vetämällä viiva suorakulmion alakulmasta vastakkaiseen kulmaan ja toistamalla se toisen alakulman kanssa. Nämä viivat leikkaavat täsmälleen kultaisen suorakulmion keskellä. Mittaa seuraavaksi jokaisen viivan puoliväli keskipisteestä alkaen. Näitä neljää pistettä kutsutaan suorakulmion silmiksi (kultainen suhde). Maalauksen pääpainopiste piirretään tai maalataan sitten näiden kiinnostuksen kohteiden (suhteiden) sisällä.
Musiikin kultainen suhde

Musiikki koostuu numeerisista arvoista ja kun kultaista suhdetta käytetään musiikkiteoksen luomiseen, siitä tulee elävä esimerkki matematiikasta. Fibonacci-sekvenssi on yleistä myös musiikissa:
- Asteikolla on kahdeksan nuottia.
- Kolmas ja viides nuotti ovat sointujen perusta.
- Jokaisen sävelen pituus tai oktaavi on 13 nuottia.
Sekvensointi jatkuu koko musiikkikappaleen ajan ja muuttuu monimutkaisemmaksi saavuttaessaan kultaisen suhteen.
Säveltäjät, jotka käyttivät kultaista lukua
Jotkut tunnetuimmista klassisista säveltäjistä, kuten Bach, Beethoven, Chopin ja Mozart, käyttivät musiikkikappaleissaan kultaista suhdetta ja Fibonacci-sekvensointia. Jotkut modernit säveltäjät, kuten Casey Mongoven, ovat tutkineet kultaista suhdetta musiikissaan.
Esimerkkejä kultaisista suhteista luonnossa

Mistä luonnossa kultainen suhde löytyy? Se on kultaisessa tai Fibonacci-spiraalissa, joka voidaan luoda käyttämällä kultaista suhdetta. Tämä on ilmiö, jota esiintyy laaj alti luonnossa. Kasvin lehdet kasvavat niin, että mahdollisimman monet voivat kiertää vartta ylöspäin. Uusi lehti muodostuu vasta sen jälkeen, kun sitä jatkanut on muodostunut.
- Spiraalikaktukset
- Spiraaligalaksit
- Auringonkukat
Kukkia Fibonacci-sekvenssillä
Joissakin kukissa on terälehdet, jotka seuraavat Fibonacci-sekvenssiä:
- Kolme terälehteä:Iris, lilja, orkideat, trillium
- Viisi terälehteä: Buttercupit, pelargoniat, hibiscus, aamukirkko, nasturtium
- Kahdeksan terälehteä: Delphiniums
- 13 terälehteä: Tietyt koirankakkaralajikkeet, ragwort, kehäkukka
Fibonacci Spiral in Pinecones

Puulajesta riippuen voit nähdä myös kultaisen suhteen toiminnassa käpyjen Fibonacci-lukusarjassa. Käpyn toiselta puolelta löytyy kahdeksan spiraalin sarja ja toiselta puolelta 13 spiraalia. Toisessa käpykuviossa on viisi spiraalia toisella puolella ja kahdeksan toisella puolella.
Kultainen suhde ihmisissä
Tämä suhde on tärkeä myös sen kann alta, miten ihmiset näkevät toisensa, vaan myös sen, miten heidän kehonsa toimii ja DNA:ssa.
DNA paljastaa kultaisen suhteen
Yksi hämmästyttävimmistä esimerkeistä kultaisesta suhteesta löytyy ihmisen DNA-rakenteesta. Tämä voidaan nähdä yhdestä DNA:n poikkileikkauksesta, joka paljastaa, että DNA:n kaksoiskierre muodostaa kymmenkulmion muodon. Tämä on kahden viisikulmion yhdistelmä, jotka on kierretty 36 astetta toisistaan ja muodostavat DNA:n kaksoiskierteen. Itse kaksoiskierteinen spiraali muodostaa viisikulmion. Jopa yksittäinen DNA-molekyyli paljastaa kultaisen leikkauksen eli jumalallisen osuuden perustan.
Math Behind the Golden Ratio
Kultaisen suhteen löytäminen tosielämässä on yksinkertaista, sillä se näkyy kaikkialla ympärilläsi. Se on matemaattinen totuus, jota käytetään määrittelemään luonnossa yleisesti tunnettu täydellinen luku, jota ihmiset ovat kopioineet ja jäljitelleet vuosisatojen ajan. Tämän numeron yksinkertainen kauneus peittää sen toteuttamisen monimutkaisuuden. Ymmärtääksesi kultaisen suhteen taustalla olevan teorian, sinun on ensin tutkittava suhteen Fibonacci-sekvensointia.
Fibonacci-sekvenssi ja kultainen suhde
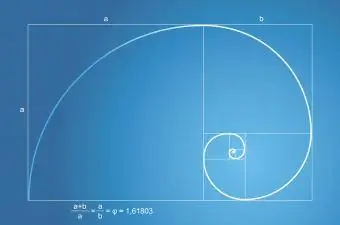
Fibonacci-sekvenssillä tai -sarjalla on suhde kultaiseen suhteeseen. Fibonacci-sarja näkyy kasvin lehtien lukumäärässä ja kukan terälehtien lukumäärässä. Fibonacci-spiraali, jota esiintyy luonnossa, on aina osa kultaista suorakulmiota, jolla on kultainen suhde.
Fibonacci-sarjan matematiikka on yksinkertaista:
- Josvio alkaa 0:lla ja 1:llä.
- Liitä vain kaksi viimeistä numeroa yhteen saadaksesi sarjan seuraavan numeron.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 ja niin edelleen.
- Tästä Fibonacci-sarjan esimerkistä tulee: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ja niin edelleen.
Fibonaccin suhde kultaiseen suhteeseen toteutuu, kun sitä lisätään eteenpäin, pidemmälle ja pidemmälle. Mitä enemmän lisäät sarjaa, sitä lähemmäs Kultaista suhdetta pääset.
Kultaisen suorakulmion ja kolmion luominen
Jos haluat luoda kultaisen suorakulmion Fibonacci-sekvenssillä, aloitat neliöstä. Aloitat suorakulmion rakentamisen lisäämällä toisen neliön alkuperäiseen neliöön. Muista käyttää kaavaa: 0+1=1 on ensimmäinen neliö, 1+1=2 - lisäät toisen neliön.1+2=3 lisäät kolme ruutua ja seuraavaksi, 2+3=5, lisäät viisi ruutua. Jatkat neliöiden lisäämistä ja lopulta muodostat kultaisen suorakulmion.
Kultainen kolmio voidaan luoda puolittämällä kultainen suorakulmio kulmasta vastakkaiseen kulmaan. Tämä luo kolmion, jossa sen kolmen sivun tai kulman suhde on 2:2:1, mikä tarkoittaa, että kaksi pitkää sivua ovat yhtä pitkiä ja lyhyt kulma on tasan puolet kahden pidemmän sivun pituudesta.
Kultainen suhde todellisessa maailmassa
Kultaista suhdetta kutsutaan usein jumalaiseksi suhteeksi, koska se on näkyvästi esillä luonnossa ja ihmiskehoissa. Havainto, että kultainen suhde on läsnä niin monissa elävissä olennoissa, edisti kunnioitusta tätä maagista suhdetta kohtaan, ja se on edelleen inspiraationa taiteilijoille ja tekijöille tänään.